Soliton's Dissipation Through Emission Of Radiation
Researchers
Project Description
Introduction
The aim is to propagate the ground state wave function of the
following nonlinear Hartree-equation in an external harmonic
potential:
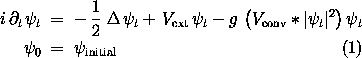
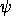 is the wave function, is the wave function,
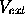 is an external potential, is an external potential,
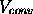 is a convolution potential (Coulomb
or Yukawa), * denotes convolution and g is a coupling constant.
There are so far no analytical solutions. Therefore we use a numerical
approach. is a convolution potential (Coulomb
or Yukawa), * denotes convolution and g is a coupling constant.
There are so far no analytical solutions. Therefore we use a numerical
approach.
Why is the NHE interesting?
Let's consider a system of bosons with weak attractive two-body
interactions.
It is proven that in the limit, where the interaction strength
vanishes, the dynamics of the system can be described by the NHE (1).
The solutions are solitary waves looking like approximate
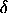 -functions.
Physically, such solutions describe bound compounds ("snow balls") of many
bosons.
In reference [1] it is shown that, under the influence of a slowly varying
external potential, the center of mass of such a compound moves along a
trajectory which is a solution of Newton's equations of motion corrected by a
very small friction term. -functions.
Physically, such solutions describe bound compounds ("snow balls") of many
bosons.
In reference [1] it is shown that, under the influence of a slowly varying
external potential, the center of mass of such a compound moves along a
trajectory which is a solution of Newton's equations of motion corrected by a
very small friction term.
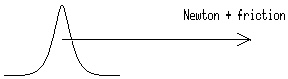
The friction causes that the compound loses energy radiating waves.
Calculation of the Ground State
First the Ground State (minimizer) is calculated in two dimensions.
The following eigenvalue-equation is solved:
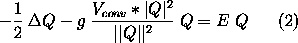
Here there is no external potential 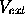 .
We consider .
We consider 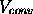 to be either a Coulomb or a Yukawa potential.
to be either a Coulomb or a Yukawa potential.
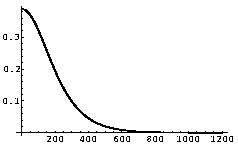
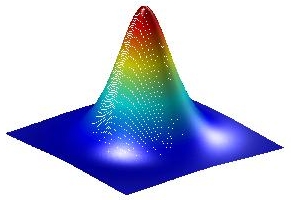
The solution has a rotational invariance, is smooth and has a global
maximum (see Fig.1).
| |
Fig 1: Radial part of the calculated minimizer and its 3-D representation.
| |
Propagation in a harmonic potential
Now the oscillation in 2-D of the minimizer in an external harmonic
potential is studied.
Thereby the decrease of the amplitude and the energy spectrum are observed.
Tool: C++ Code of W. Aschbacher.
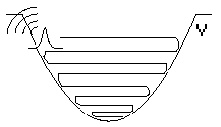
Problem: Absorbing Boundaries
Solution: Negative imaginary potential on some boundary strip:
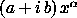
Parameters to determine: a, b,
 , number of absorbing layers. , number of absorbing layers.
Run simulations on Asgard with different values of the parameters:
- Absorption of a sequence of Gaussian wave packets with different initial momenta.
- Absorption of the radiation stemming from a minimizer with vanishing
initial momentum.
- Propagation of the Minimizer in an external harmonic potential.
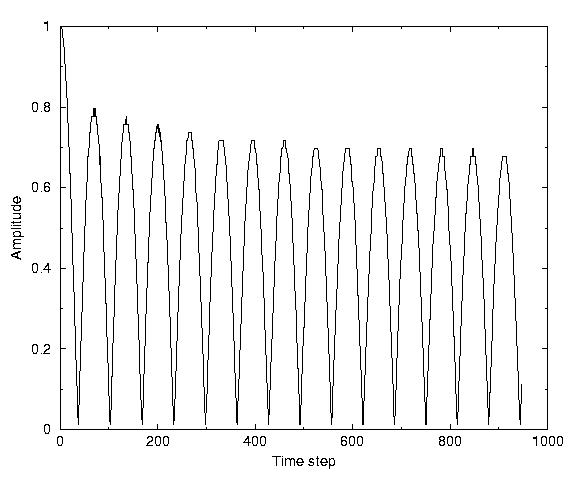
The following picture shows the results obtained so far.
| |
Fig 2: The amplitude of the oscillation of the minimizer in an external
harmonic potential well as a function of time for a 2-D grid with 256
grid points in each direction. The y-axis shows the quotient of the
actual amplitude (= distance from the minimum of the potential) and the initial
amplitude. |
|
We observe a decrease of the amplitude as a function of the time
steps. We expect that if the simulation time is much greater, one should be
able to see the minimizer oscillating into the minimum of the potential.
CLICK ON THIS LINK TO SEE A NICE FILM OF THE RESULTS.
Publications
Gianluca Interlandi, Soliton's Dissipation Through Emission Of
Radiation, Diploma Thesis, September 2000.
References
[1] Jürg Fröhlich, Tai-Peng Tsai, Horng-Tzer Yau, On the
point-particle (Newtonian) limit of the non-linear Hartree
equation.
Written by: Gianluca
Interlandi <gianluca@student.ethz.ch>
| 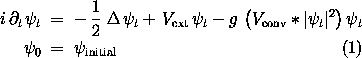
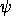 is the wave function,
is the wave function,
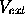 is an external potential,
is an external potential,
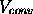 is a convolution potential (Coulomb
or Yukawa), * denotes convolution and g is a coupling constant.
There are so far no analytical solutions. Therefore we use a numerical
approach.
is a convolution potential (Coulomb
or Yukawa), * denotes convolution and g is a coupling constant.
There are so far no analytical solutions. Therefore we use a numerical
approach.
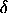 -functions.
Physically, such solutions describe bound compounds ("snow balls") of many
bosons.
In reference [1] it is shown that, under the influence of a slowly varying
external potential, the center of mass of such a compound moves along a
trajectory which is a solution of Newton's equations of motion corrected by a
very small friction term.
-functions.
Physically, such solutions describe bound compounds ("snow balls") of many
bosons.
In reference [1] it is shown that, under the influence of a slowly varying
external potential, the center of mass of such a compound moves along a
trajectory which is a solution of Newton's equations of motion corrected by a
very small friction term.

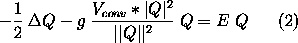



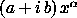
 , number of absorbing layers.
, number of absorbing layers.